© 2025 Astra.si. Wszelkie prawa zastrzeżone.
Dla następnego pokolenia.
© 2025 Astra.si. Wszelkie prawa zastrzeżone.
Dla następnego pokolenia.
W analizie matematycznej jednym z kluczowych pojęć jest to, które opisuje zmianę funkcji względem zmiany jej argumentu. To pojęcie prowadzi do formalnej definicji pochodnej, która jest podstawą dla wielu dalszych konstrukcji i teorii matematycznych. Centralna idea polega na tym, że pochodna mierzy tempo zmian funkcji w danym punkcie – czyli jak szybko i w którym kierunku funkcja tam się zmienia.
Niech 'f' będzie dowolną funkcją rzeczywistą, a x₀ pewnym punktem w jej dziedzinie. Pochodna funkcji 'f' w punkcie x₀ jest oznaczana jako f'(x₀) i jest zdefiniowana jako granica ilorazu różnicowego, jeśli ta granica istnieje:
f'(x₀) = lim (gdy h → 0) [f(x₀ + h) - f(x₀)] / h.
W tym wyrażeniu 'h' reprezentuje małą zmianę w zmiennej niezależnej x, podczas gdy licznik pokazuje zmianę wartości funkcji. Jeśli ta granica istnieje, mówimy, że funkcja jest różniczkowalna w tym punkcie.
Geometrycznie pochodna reprezentuje nachylenie stycznej do wykresu funkcji w punkcie x₀. Jeśli wyobrazimy sobie wykres funkcji jako gładką krzywą, to styczna w danym punkcie wskazuje kierunek, w którym krzywa zmierza. Im większa pochodna, tym bardziej strome to nachylenie.
Użyjmy definicji:
f'(x) = lim (gdy h → 0) [(x + h)² - x²] / h = lim (gdy h → 0) [x² + 2xh + h² - x²] / h = lim (gdy h → 0) [2xh + h²] / h = lim (gdy h → 0) (2x + h) = 2x.
Dlatego pochodna funkcji x² wynosi 2x. Oznacza to, że wartości tej funkcji w punkcie x zmieniają się w tempie 2x.
Pochodna jest matematycznym narzędziem do opisywania tempa zmian funkcji. Używając granicy ilorazu różnicowego, dochodzimy do precyzyjnej definicji, która ma zarówno znaczenie liczbowe, jak i geometryczne. Rozumiejąc podstawowe przykłady, takie jak funkcja kwadratowa, możemy łatwiej budować wiedzę o bardziej złożonych funkcjach.
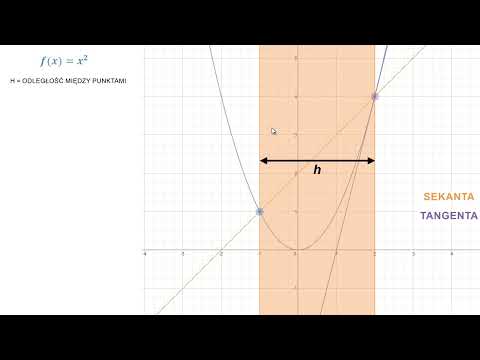
Czym jest pochodna?
Wyjaśnienie
13 minut
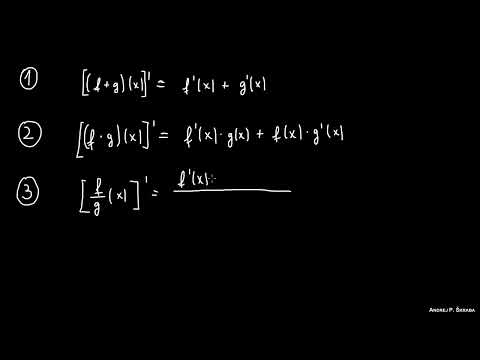
Reguły różniczkowania
Wyjaśnienie
4 minuty
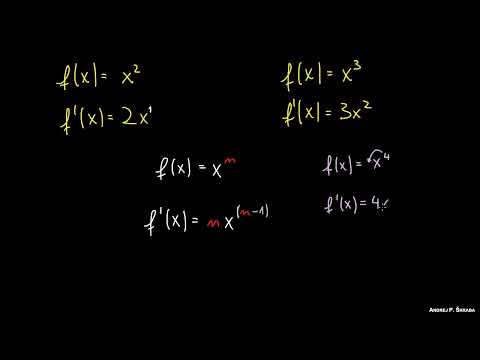
Reguły obliczania pochodnej funkcji
Wyjaśnienie
5 minut
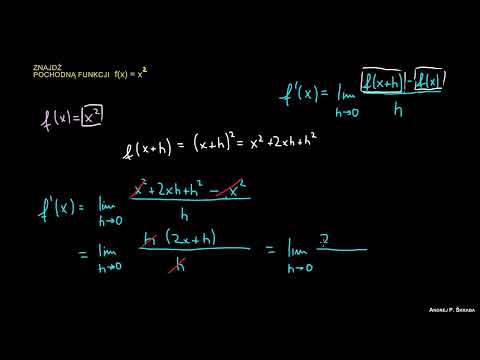
Pochodna z definicji 1
Wyjaśnienie
6 minut
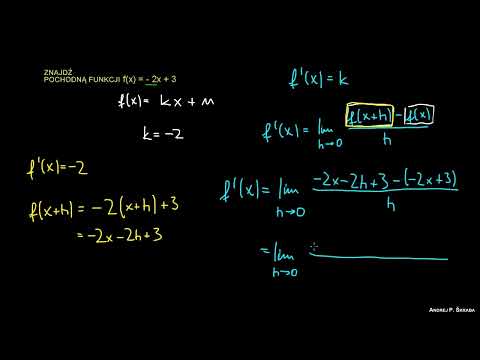
Pochodna z definicji 2
Wyjaśnienie
5 minut
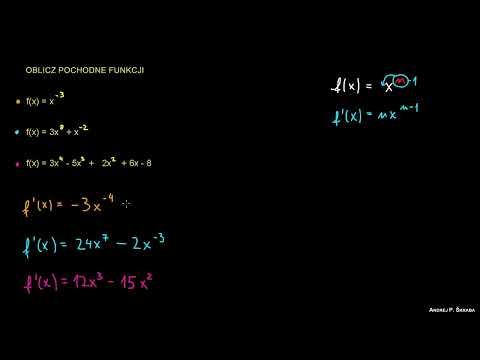
Pochodna - ćwiczenie 1
Wyjaśnienie
5 minut

Pochodna - ćwiczenie 2
Wyjaśnienie
4 minuty

Pochodna - ćwiczenie 3
Wyjaśnienie
4 minuty